你还记得上一次心灵感应的那个扑克牌魔术吗？老杰克和小杰克爷俩儿“合伙作案”，五张扑克牌把观众弄得一头雾水。可是你听说了吗，最近老杰克和小杰克吵起来了，小杰克不甘心总是给父亲当助手，想上舞台来一次个人专场表演，可是老杰克不答应，认为小杰克还太年轻了。小杰克自然也不甘示弱，上一回两人一起用五张扑克牌“心灵感应”，这一次我用四张扑克牌，以个人表演，和观众来个心灵感应，咱爷俩儿谁怕谁呀！

    表演开始了，小杰克上场后先把准备好的四张扑克牌，红桃A,红桃2，红桃3，红桃4，从左到右依次摆到桌面上。台下观众心里不禁想，这小家伙准备干什么呢？看起来他怎么有点像幼儿园里教算术的老师呢？

    接着，小杰克像往常一样在现场找了一位观众，然后对大家说，“今天我要读出你心中的一二三四”，“现在我背过身去，然后你在1、2、3、4四个数字中你选择一个最喜欢的，然后把这张数字的牌和红桃A互相交换位置，比如你选了红桃2，就要把红桃2放到红桃A的位置上，把红桃A放到红桃2的位置上，大家一定要记住这张牌。当然你如果最喜欢的牌正是红桃A，就什么也不用做了。这位观众想了想，选择了红桃3。

    之后，魔术师小杰克说，“现在请你把四张牌都翻过去，然后，从左到右把四张牌叠到一起，最左面的那张牌自然放到最下面”。等着这位观众把扑克牌收好之后，小杰克转过身来，“好了，四张扑克牌都在你的手中，我什么也看不到。为了让你选的那张牌藏的毫无踪迹，下一步就是要把这四张牌洗乱，那么怎么洗呢？这样，你每次从这叠牌的上面取一张、两张或者三张牌放到牌的最低下，经过十次“翻江倒海”之后，这四张牌的顺序一定完全打乱了，现在就开始吧”。这位观众按照要求把手中的几张牌洗来洗去，结束后交给了小杰克。“现在我把已经经历了“干洗机清洗”的四张扑克牌放到重新放到桌面子上”，他轻轻地用手翻开最上面的一张牌，是红桃2，摆在了最左面，然后把接下来的三张牌依次摆在的后面。此时台下观众眼睛一望，四张牌的确已经和开始的时候顺序完全不一样了。

    小杰克随后伸出双手，在四张牌的上面挥舞一番，施加起了他的“魔法”。然后神秘兮兮地对这位观众说道，“你选的牌一定不是2，也不是A，只剩下了两张牌，3和4。我的第六感觉告诉我，你选的牌一定是这两张中的红桃3”随后台下观众中响起一阵热烈的掌声，小杰克成功的答对了这道“四选一”的选择题。

    读到这里，很到人要问，小杰克这项阅读别人心中一二三四的超能力是怎么来的呢？我要是有他的这项能力就好了，以后每次考试，和学习好的同学来一次“超能力”，选择题就不愁了，ABCD一个也错不了。

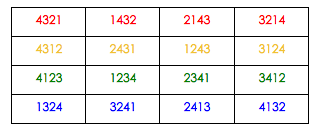
    你可能会说这位观众是小杰克的“托”，但是小杰克可以一千个一万个保证的是，观众一定是任意找的。说起来，谜底并不复杂，请看以下这张图，如果最后小杰克放到桌子上的四张牌的顺序在红色的方格里，那么就可以断定，观众选的牌是红桃A，如果是在黄色的区域内，就一定是红桃2，绿色的方格内呢？一定是红桃3。蓝色的方格内，不用说了，红桃4。小杰克脑子里记住这张图就可以了。如果最后桌子上的牌不是这十六种之列怎么办？那一定是这位观众太淘气了，没有按照小杰克的要求去做。

    有一个有趣的问题：这四张牌摆成一行，一共有多少种可能呢？计算方法是4乘以3乘以2再乘以1，一共是24种，不过在魔术里，如果不出错的话，有8种永远也不会看到。那么一副牌54张牌排成一列的话，一共有多少中可能性呢？聪明的你一定可以猜到，算法是54乘以53，再乘以52，得到的结果再乘以51，……，最后再乘以2，得到的结果有多大呢？23后面有71个0，这个数字大到了难以想象。也就是说每一次你把一副洗好的扑克牌（当然不是像小杰克这样作弊）一张张摆开，几乎不可能出现两列完全相同的牌。

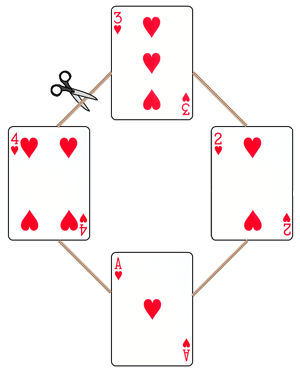
    回到正题，你可能会问，“咦，这是怎么回事？魔术中扑克牌不是都被洗乱了吗？”小杰克说，“非也非也，听我慢慢道来”，“最开始的时候，观众选的是红桃3，和红桃A换完位置之后，是这样的，我们把这四张牌围成一个圆圈，我得翻江倒海洗牌大法表面上可以把扑克牌变得乱七八糟，可是实际上仔细想一想，不管每一次从牌的上面拿几张放到最下面，要不管一共拿多少次，只是相当于在旋转这个圈，四张牌的相对位置，左邻右舍都没有变，所以无论任何时候，这副牌都相当于把这条链子剪开，所以一定在这四种可能性之中。”

    “可是故事还没有完，为了进一步迷惑观众，最开始收牌的时候最左面的牌是放在最下面，可是最后把牌放回桌子上的时候是把最上面的牌放到最左面，这样四张牌的顺序就开始的时候倒过来了，一二三四变成了四三二一，让人相信牌是洗过的。”

以后，你也像小杰克一样，给你的朋友来做一道四选一选择题吧。

(本文的删节版同时已发表于果壳网)