醉汉,赌徒和爱因斯坦
来源:科学松鼠会 日期:2015-08-03

1905年是值得物理学界记住的一年。这一年爱因斯坦发表了五篇学术论文,每一篇都起码是一个里程碑式的工作。除了著名的狭义相对论、光电效应之外,有一篇题为《关于热的分子运动论所要求的静止液体中悬浮小粒子的运动》的文章[1],主要研究了布朗运动的规律。布朗运动得名于英国的植物学家劳伯.布朗(Robert Brown),他在1827年发现悬浮于水中的花粉颗粒会做连续快速的不规则移动。后来物理学家将这种运动形式称为随机行走(random walk)。进行这种运动,就象打醉拳一样,每一步的方向都飘忽不定,完全随机(见下图)。统计物理的实验和理论都告诉我们,起始于同一点的随机行走在一段时间之后位于任何方向的可能性都是一样的,而且平均远离起始点的距离正比于时间的平方根。随机行走这个物理问题和醉汉、赌徒都有关系,和网络搜索引擎(比如Google)也有关系,在很多领域都有着重要的应用。
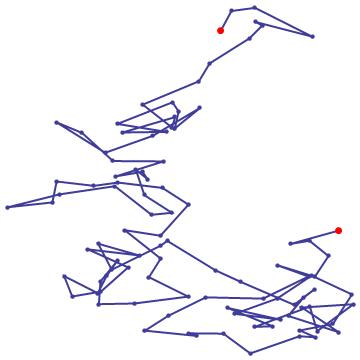
随机行走轨迹图
在讲述随机行走的理论的时候,物理学家们常用醉汉作为例子。平直的说,这里的醉汉是指喝到不知东南西北又尚可以行动的“理想醉汉”。在书呆子看来,这样的比喻易于想象又富有趣味。这样的一个理想醉汉的行走轨迹就是完全的随机行走。前面提到的统计物理实验和理论的结果可以这样理解:醉汉走了25步之后,很有可能只移动了相当于清醒状态下5步的距离,并且移动的方向也是“一切皆有可能”。因此,我们应该可以理解在日常生活中,醉汉自己能够从酒馆成功回到家的可能性是很低的,而且离家越远几率越低,即使能回到家,花的时间也会远超过正常所需:屡见不鲜的醉汉栖息于花圃、出租车等地的报道也就不足为怪了。
再来看看赌徒的问题。
如果赌场和赌徒之间的博弈是一个公平的游戏,那么赌徒获胜的可能性有多大?可能每一个成功或者不成功的赌徒对这个问题都有他们各自不同的看法。也可能更多的人出于实际的考虑对这个问题的合理性有着质疑。但是,作为起始于赌徒和赌场间激动人心小游戏的一门学科,统计物理利用随机行走的结果对这个问题有着科学的回答。
让我们把这个游戏描述的再清楚一点:如果有两个赌徒,甲赌徒有A块钱,乙赌徒有B块钱,他们之间进行一个公平的游戏,每次各有50%的几率赢,每次输家给赢家一块钱,不到一方输光所有的钱不停手,那么各自获胜的几率是多少?这个问题可以等效为一个一维的随机行走问题,就像下图表现的那样:行走在一条笔直街道上的醉汉,甲赢一次则代表醉汉向右走一步,乙赢一次则向左走一步,从左边或者右边离开的几率各是多少?计算的过程比较复杂,但是结果很简单,甲和乙各自获胜的几率比是A:B。因此,如果一个赌徒拿着100块钱去和有着900块钱的赌场进行这种公平的游戏,那么赌徒有10%的可能性获胜。那么实际的情况呢?赌场和赌徒的钱数差别比这大得多,赌徒获胜的希望微乎其微。理性的赌徒或许会给自己设定一个合理的目标,比如自己有100块的话,赢50块就收手。那么,赌徒和赌场的输赢几率比就是2:1,将会是一个不亏不赚的结果。但是,考虑到赌场一般会从赌徒赢的钱里面抽头,赌徒总是会亏的。更别提赌场可以通过规则的设定,以及辅助于各种原始的或者高科技的小技巧改变游戏的公平性。幻想从赌场赚钱的人可以回家反省了。
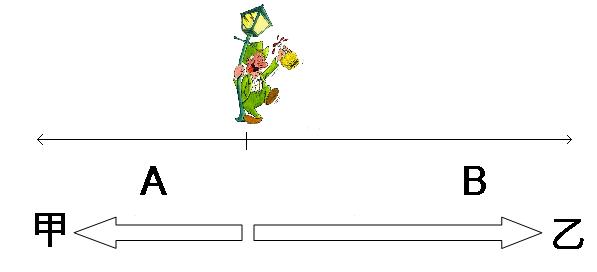
赌徒问题和一维随机行走
听说过一个八卦,说是有一年的美国物理年会是在拉斯维加斯召开的。拉斯维加斯提供了非常好的服务--毕竟是专业的服务场所么。然后晚上的时候物理学家们就去赌场了。出乎赌场意料的是,物理学家们只观战不下场,结果年会期间拉斯维加斯的赌场损失了一大笔钱,很不高兴。然后美国物理年会就再也没能在那里举行过。讲这个故事的,是一个做统计物理的教授。为什么统计物理的教授不去赌钱呢?因为他们怕输,而且知道自己必输无疑!
随机行走在很多领域里都有重要的应用,我们简单举几个例子:在生态学中,它被用来模拟生物个体的移动和种群的数量变化;化学家用它的结果来研究聚合物的性质;计算机学家用它来估计因特网的大小。另外一个有名的例子就是Google的网页排名:Google备份了整个因特网,在上面随机地放了很多很多由电脑控制的小程序,称为虚拟访问者(random surfer), 这些访问者随机的选择所在网页的某一个链接,跳到另外的网页上去,同时,电脑程序记录下来每个网页被访问者“访问”的次数。如果把每个网页看成一个点,网页之间的链接用连接两个点的线表示,那么虚拟访问者就在这个网络里做着随机行走。一个网页被其他的网页链接得次数越多,就有越高的可能性被访问,在网络里 也越重要。这样,被访问的次数越多就说明了网络对这个页面的关注越大,因此网页的排名就可以通过虚拟访问者的随机访问而计算出来了(参考阅读:flyheller的《google炸弹,你玩过了么?》)。
[1]. Einstein, Albert; R. Fürth, transl. by A. D. Cowper (1926, reprinted in 1956). "On the Movement of Small Particles Suspended in a Stationary liquid Demanded by the Molecular-Kinetic Theory of Heat".
感谢水龙吟、四月、圆儿、Fujia、拇姬、候戏、Albert_JIAO 、Ent、小庄和游识猷对本文的帮助。