怎样计算用单循环制进行的比赛场数?
来源:新华网 日期:2018-07-10
用淘汰制进行的比赛需要的比赛场次较少,并且因为每一轮的不同比赛可以在不同场地同时进行,因而用时较短,所以当报名人数较多时,淘汰赛制是一个很不错的选择。但是淘汰赛制有一个很明显的缺点,如果两名实力较强的参赛者较早相遇,那么淘汰赛所产生的结果便有了一些遗憾。因此,在参赛者人数较少时,通常使用相对更为公平的、更能合理判断参赛者水平的循环赛制。
循环赛制,包括单循环、双循环和分组循环三种方法。本文主要介绍单循环赛制。
在单循环赛中,每一名参赛者都会与其他参赛者各比赛一次,与之类似的还有双循环赛,每一名参赛者会与其他参赛者各比赛两次,最后以胜负场积分判定参赛者名次。理论上,循环赛是从固定的已知参赛者中决出冠军的最好方式,因为对每一名参赛者而言,面对所有对手的机会都是均等的,这也给了参赛者们状态不佳等不利于比赛结果因素的“容错率”。这样的比赛结果也会更准确且更具有说服力,因此,经历循环赛制胜利的冠军通常被公认为最强者。
我们假设有14名参赛者参与单循环制进行的比赛,这种情况下,每一名参赛者都要与除了自己以外的其他所有对手进行一场比赛,也就是14×13=182场,但由于比赛的双方仅仅进行一场比赛,还需要将上一步的总场数除以2,也就是最终需要进行的比赛场次为91场。化用到一般情况下,也就是当有n名参赛者参与单循环制进行的比赛时,需要进行的总场次为。
但事实上,我们从上面的计算中可以看出,即使参与比赛的选手数量不多,需要进行的比赛场次却很多,这无疑拉长了赛程,增加了比赛成本。在这一前提下,通常根据参赛者的数量将其分为两组、三组或四组进行比赛,决出各个小组的冠军后再进行小组冠军之间的单循环比赛,这种分组的方式通常被称为赛区,这种基于单循环制的赛制通常被称为分组单循环制。
我们仍以14名参赛者为例,将其分为两组,每组7名参赛者。
此时需要进行两轮比赛,第一轮决出各个小组的冠军,场次为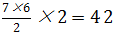 ;第二轮决出小组冠军之间的总冠军,场次为
;第二轮决出小组冠军之间的总冠军,场次为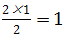 ;总场次为43场。对于更一般的情况,将n名参赛者分为m个小组(n能够被m整除),总场次应为
;总场次为43场。对于更一般的情况,将n名参赛者分为m个小组(n能够被m整除),总场次应为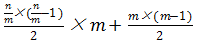 即
即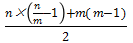 。对比上文未分组的单循环赛制,我们可以很明显地看出分组单循环制比单循环制的场次更短、效率更高,并且也能在一定程度上保证比赛的公平性。因此,分组单循环赛制是很多大型比赛首选的比赛模式。
。对比上文未分组的单循环赛制,我们可以很明显地看出分组单循环制比单循环制的场次更短、效率更高,并且也能在一定程度上保证比赛的公平性。因此,分组单循环赛制是很多大型比赛首选的比赛模式。